Beginner tutorial to ASM hacking *in progress* (written by: Zodiac )

You may have heard the MIPS assembly language is hard to learn. Or perhaps it seemed hard to you. Well this is completely false. Learning MIPS assembly is easy, putting it in practice whoever might be hard for a lot of people who have an undeveloped logical mind.


HEXADECIMAL AND BINARY

Now let’s start with Hex.
Hex is a base 16 number system while Decimal is base 10.

While Decimal contains:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Hex has 6 more:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Binary	Hex	Dec		Binary	Hex	Dec		Binary	Hex	Dec		Binary	Hex	Dec
00000000	0x00	0		01000000	0x40	64		10000000	0x80	128		11000000	0xC0	192
00000001	0x01	1		01000001	0x41	65		10000001	0x81	129		11000001	0xC1	193
00000010	0x02	2		01000010	0x42	66		10000010	0x82	130		11000010	0xC2	194
00000011	0x03	3		01000011	0x43	67		10000011	0x83	131		11000011	0xC3	195
00000100	0x04	4		01000100	0x44	68		10000100	0x84	132		11000100	0xC4	196
00000101	0x05	5		01000101	0x45	69		10000101	0x85	133		11000101	0xC5	197
00000110	0x06	6		01000110	0x46	70		10000110	0x86	134		11000110	0xC6	198
00000111	0x07	7		01000111	0x47	71		10000111	0x87	135		11000111	0xC7	199
00001000	0x08	8		01001000	0x48	72		10001000	0x88	136		11001000	0xC8	200
00001001	0x09	9		01001001	0x49	73		10001001	0x89	137		11001001	0xC9	201
00001010	0x0A	10		01001010	0x4A	74		10001010	0x8A	138		11001010	0xCA	202
00001011	0x0B	11		01001011	0x4B	75		10001011	0x8B	139		11001011	0xCB	203
00001100	0x0C	12		01001100	0x4C	76		10001100	0x8C	140		11001100	0xCC	204
00001101	0x0D	13		01001101	0x4D	77		10001101	0x8D	141		11001101	0xCD	205
00001110	0x0E	14		01001110	0x4E	78		10001110	0x8E	142		11001110	0xCE	206
00001111	0x0F	15		01001111	0x4F	79		10001111	0x8F	143		11001111	0xCF	207
00010000	0x10	16		01010000	0x50	80		10010000	0x90	144		11010000	0xD0	208
00010001	0x11	17		01010001	0x51	81		10010001	0x91	145		11010001	0xD1	209
00010010	0x12	18		01010010	0x52	82		10010010	0x92	146		11010010	0xD2	210
00010011	0x13	19		01010011	0x53	83		10010011	0x93	147		11010011	0xD3	211
00010100	0x14	20		01010100	0x54	84		10010100	0x94	148		11010100	0xD4	212
00010101	0x15	21		01010101	0x55	85		10010101	0x95	149		11010101	0xD5	213
00010110	0x16	22		01010110	0x56	86		10010110	0x96	150		11010110	0xD6	214
00010111	0x17	23		01010111	0x57	87		10010111	0x97	151		11010111	0xD7	215
00011000	0x18	24		01011000	0x58	88		10011000	0x98	152		11011000	0xD8	216
00011001	0x19	25		01011001	0x59	89		10011001	0x99	153		11011001	0xD9	217
00011010	0x1A	26		01011010	0x5A	90		10011010	0x9A	154		11011010	0xDA	218
00011011	0x1B	27		01011011	0x5B	91		10011011	0x9B	155		11011011	0xDB	219
00011100	0x1C	28		01011100	0x5C	92		10011100	0x9C	156		11011100	0xDC	220
00011101	0x1D	29		01011101	0x5D	93		10011101	0x9D	157		11011101	0xDD	221
00011110	0x1E	30		01011110	0x5E	94		10011110	0x9E	158		11011110	0xDE	222
00011111	0x1F	31		01011111	0x5F	95		10011111	0x9F	159		11011111	0xDF	223
00100000	0x20	32		01100000	0x60	96		10100000	0xA0	160		11100000	0xE0	224
00100001	0x21	33		01100001	0x61	97		10100001	0xA1	161		11100001	0xE1	225
00100010	0x22	34		01100010	0x62	98		10100010	0xA2	162		11100010	0xE2	226
00100011	0x23	35		01100011	0x63	99		10100011	0xA3	163		11100011	0xE3	227
00100100	0x24	36		01100100	0x64	100		10100100	0xA4	164		11100100	0xE4	228
00100101	0x25	37		01100101	0x65	101		10100101	0xA5	165		11100101	0xE5	229
00100110	0x26	38		01100110	0x66	102		10100110	0xA6	166		11100110	0xE6	230
00100111	0x27	39		01100111	0x67	103		10100111	0xA7	167		11100111	0xE7	231
00101000	0x28	40		01101000	0x68	104		10101000	0xA8	168		11101000	0xE8	232
00101001	0x29	41		01101001	0x69	105		10101001	0xA9	169		11101001	0xE9	233
00101010	0x2A	42		01101010	0x6A	106		10101010	0xAA	170		11101010	0xEA	234
00101011	0x2B	43		01101011	0x6B	107		10101011	0xAB	171		11101011	0xEB	235
00101100	0x2C	44		01101100	0x6C	108		10101100	0xAC	172		11101100	0xEC	236
00101101	0x2D	45		01101101	0x6D	109		10101101	0xAD	173		11101101	0xED	237
00101110	0x2E	46		01101110	0x6E	110		10101110	0xAE	174		11101110	0xEE	238
00101111	0x2F	47		01101111	0x6F	111		10101111	0xAF	175		11101111	0xEF	239
00110000	0x30	48		01110000	0x70	112		10110000	0xB0	176		11110000	0xF0	240
00110001	0x31	49		01110001	0x71	113		10110001	0xB1	177		11110001	0xF1	241
00110010	0x32	50		01110010	0x72	114		10110010	0xB2	178		11110010	0xF2	242
00110011	0x33	51		01110011	0x73	115		10110011	0xB3	179		11110011	0xF3	243
00110100	0x34	52		01110100	0x74	116		10110100	0xB4	180		11110100	0xF4	244
00110101	0x35	53		01110101	0x75	117		10110101	0xB5	181		11110101	0xF5	245
00110110	0x36	54		01110110	0x76	118		10110110	0xB6	182		11110110	0xF6	246
00110111	0x37	55		01110111	0x77	119		10110111	0xB7	183		11110111	0xF7	247
00111000	0x38	56		01111000	0x78	120		10111000	0xB8	184		11111000	0xF8	248
00111001	0x39	57		01111001	0x79	121		10111001	0xB9	185		11111001	0xF9	249
00111010	0x3A	58		01111010	0x7A	122		10111010	0xBA	186		11111010	0xFA	250
00111011	0x3B	59		01111011	0x7B	123		10111011	0xBB	187		11111011	0xFB	251
00111100	0x3C	60		01111100	0x7C	124		10111100	0xBC	188		11111100	0xFC	252
00111101	0x3D	61		01111101	0x7D	125		10111101	0xBD	189		11111101	0xFD	253
00111110	0x3E	62		01111110	0x7E	126		10111110	0xBE	190		11111110	0xFE	254
00111111	0x3F	63	01111111	0x7F	127	10111111	0xBF	191	11111111	0xFF	255

You can be sure a number is in hex when it is preceded by 0x, or $ which are commonly used in programming communities:
0xFF, 0x024E, $A2

The most commonly used format in hex is a byte.
A byte is composed of 2 nibbles. Those nibbles are simply a character from 0 to F.
Those nibbles are composed of bits. While bits and Boolean are stored the exact same way, we use the term Boolean for a value that is either TRUE (1) or FALSE (0) and a bit is simply 1 or 0.

Range of values	Type	Equivalent
0-1	Boolean/Bit	-
0x0-0xF	Nibble	4 bits
0x00-0xFF	Byte	8 bits
0x0000-0xFFFF	Half-Word	2 bytes
0x00000000-0xFFFFFFFF	Word	4 bytes
0x0000000000000000-0xFFFFFFFFFFFFFFFF	Double-Word	2 words

There are others, but that’s not important for PSX hacking.

An important note about the Little Endian (the data format the PSX uses) is that the bytes are reversed. What this means is that the last byte in a value becomes the first. Note that this strictly depends of the value type; hence how the value is read/written. Note that the following examples show the stored values in hex display without 0x or $, which is because those characters would not only be confusing but would also take a lot of space. Whoever in person to person written conversations, 0x or $ should ALWAYS be used to avoid confusion with a decimal value.

Hexadecimal Value	Is stored as
0x78	78
0x011F	1F 01
0x80050263	63 02 05 80
0x00000002846A0507	07 05 6A 84 02 00 00 00

Usually the game also reads/write bits this way.

The binary 10000000 represent 0x80 in hex. This “1” will be the first bit to be loaded. In order it loads the value 0x80, 0x40, 0x20, 0x10, 0x08, 0x04, 0x02 and finally 0x01.

0	FALSE
1	TRUE

Let’s do a little hex conversion practice to help you understand better:

0x02A7 to decimal (hex is base 16)

$00 × 163 = 0 × 4096 = 0 $02 × 162 = 2 × 256 = 512 $0A × 161 = 10 × 16 = 160 $07 × 160 = 7 × 1 = 7 0 + 512 + 160 + 7 = 679

0x02A7 = 679

STATIC VS DYNAMIC

A static value doesn’t change, it is meant to be only loaded. All opcodes (which you will see later) are static. You COULD make some opcodes dynamic but this is seriously asking for trouble unless you are a high level hacker, perfectly sure of what you’re doing and know it will use less space (if that is even possible) than conventional coding.
Examples of static data: the WP of a weapon, the HPM of a job, the coordinates of a move-find item, etc.

A dynamic value is meant to be changed; therefore a new value will overwrite the previous one.
Examples of dynamic data:
HP of a unit, Max HP of a unit (base max HP calculated, different units, level up, etc.), total gil amount, etc.

A memory editor will help you finding dynamic data only. If you search for static data you’re better off using a simple hex editor. Using the memory editor you scan a first time inputting what you know of the value, change the value in game, and make another search with the known modifications to the value.
To search for static data, you can either guess what the data is for, or debug using breakpoints on the data.


SIGNED AND UNSIGNED

A signed variable can have half of its values positive, and the other half negative. How do we know if a value is signed or not? This all depends on how the value is read/written by opcodes.
Let me show you can example:
0x7F (maximum positive value of a signed byte) = 127
Nothing changed here. However:
0xFF = -1
Now I’ve got you confused. You see, while 0x7F is the highest positive value, the value right after which is 0x80 is the lowest negative value.
0x7F = +127
0x80 = -128

An unsigned byte (which is a normal byte) can have values from 0-255 (x00-xFF).

Let’s to it with 0x9B
255+1 =256
0x9B – 256 = 155 – 256 = -101
a signed 0x9B = -101, an unsigned 0x9B = 155
Remember that the value will only be negative if it exceeds half of its maximum value.

Of course, the same applies to other variables, except bits.

Value	Unsigned	Signed
0x70	112	+112
0x9F	159	-97
0x03E7	999	+999
0xFFB2	65458	-78
0x000000FE	254	+254
0x80196804	2149148676	-2145818620

OPCODES

Opcodes are the instructions executed by the console’s processor. Since we started with hexadecimal and binary, we’ll look into the bitwise operands first.
Opcodes will read/write registers depending on what it is supposed to do. Mainly we will work with conditional jumps (branches), jumps, load/write value (from/to memory), and everything else that alters a register’s value.


Many instructions have an immediate form, such as addiu (Add Immediate Unsigned) instead of addu (Add Unsigned). An immediate is a half-word value that is within the instruction itself and is static.
Some instructions have the variable form, such as SLLV (Shift Left Logical Variable) which is simply the register version of the SSL (which uses a 5 bit immediate).
A register is the type of data used by almost all instructions. They are words (so 4 bytes).
There are 32 main registers that are directly used by opcodes: r0, r1, r2, ... r31. r0 will always be 0x00000000 so you can use it to compare if a value is true or not safely.

Let’s get on to bitwise operands:

AND returns TRUE to rd if both bits in rs and rt are TRUE. Else it returns FALSE.

AND rd, rs, rt [rd = rs AND rt] AND rd, 0x00678460, 0x8005CE40 rs 00000000011001111000010001100000 0x00678460 rt 10000000000001011100111001000000 0x8005CE40 ---------------------------------------------- rd 00000000000001011000010001000000 0x00058440

ANDI rt, rs, imm. [rt = rs AND imm.] ANDI rd, 0x0000006B, 0x02C6 rs 00000000000000000000000001101011 0x0000006B im ················0000001011000110 ····0x02C6 ---------------------------------------------- rd 00000000000000000000000001000010 0x00000042

OR returns TRUE to rd if at least one of the bits in rs and rt are TRUE. Else it returns FALSE.

OR rd, rs, rt [rd = rs OR rt] OR rd, 0x00057A46, 0x0C82 rs 00000000000001010111101001000110 0x00057A46 rt 00000000000000000000110010000010 0x00000C82 ---------------------------------------------- rd 00000000000001010111111011000110 0x00057EC6

ORI rd, rs, imm. [rd = rs OR imm.] ORI rd, 0x0000006B, 0x000002C6 rs 0000000000000000000000001101011 0x0000006B im ················000001011000110 ····0x02C6 --------------------------------------------- rd 0000000000000000000001011101111 0x000002EF

SLL shifts rt's bits to the left by sa bits and stores the result in rd. Excessive bits will be destroyed. New bits are always FALSE. sa can hold a value from 0x00 to 0x1F inclusively.

SLL rd, rt, sa [rd = rt << sa] SLL rd, 0x000008E4, 0x02 rt 00000000000000000000100011100100 0x000008E4 sa ···························00010 ······0x02 ---------------------------------------------- rd 00000000000000000010001110010000 0x00002390

SLLV rd, rt, sa [rd = rt << rs] SLL rd, 0x0000008A, 0x00000004 rt 00000000000000000001010110001010 0x0000158A rs 00000000000000000000000000000100 0x00000004 ---------------------------------------------- rd 00000000000000010101100010100000 0x000158A0

SRL shifts rt's bits to the right by sa bits and stores the result in rd. Excessive bits will be destroyed. New bits are always FALSE. sa can hold a value from 0x00 to 0x1F inclusively.

SRL rd, rt, sa [rd = rt >> sa] SRL rd, 0x000012C7, 0x07 rt 00000000000000000001001011000111 0x000012C7 sa ···························00111 ······0x07 ---------------------------------------------- rd 00000000000000000000000000100101 0x00000025

SRLV rd, rt, rs [rd = rt >> rs] SRLV rd, 0x000000C3, 0x00000001 rt 00000000000000000000000011000011 0x000000C3 rs 00000000000000000000000000000000 0x00000001 ---------------------------------------------- rd 00000000000000000000000001100001 0x00000061

A few mathematic functions can be applied to registers. Many of them have a signed/unsigned version so make sure you choose the right one depending on your needs.
some of them also uses the hi(high) and lo(low) registers. Basically you cannot use those registers directly as they are not part of the 32 first registers.
However you can still move a value/from to those registers in your hacks to store temporarly a value, which can be extremely useful in some cases if you want to avoid loading/writing to the game's memory.

Here are some mathematical functions:

ADD will add the value, positive or negative, of rs to rt and store the result in rd.

ADD rd, rs, st [rd = rs + rt] ADD rd, 0x8005A48C, 0x000002B0 rs 10000000000001011010010010001100 0x8005A48C rt 00000000000000000000001010110000 0x000002B0 ---------------------------------------------- rd 10000000000001011010011100111100 0x8005A73C

ADDU rd, rs, st [rd = rs + rt] ADDU rd, 0x00000034, 0x80067F80 rs 00000000000000000000001000110100 0x00000234 rt 10000000000001100111111110000000 0x80067F80 ---------------------------------------------- rd 10000000000001101000000110110100 0x800681B4

ADDI rd, rs, imm. [rd = rs + imm.] ADDI rd, 0x0000187E, 0xFFE2 rs 00000000000000000001100001111110 0x0000187E im ················1111111111100010 ····0xFFE2 ---------------------------------------------- rd 00000000000000000001100001100000 0x00001860

ADDIU rd, rs, imm. [rd = rs + imm.] ADDIU rd, 0x0074FF80, 0xC800 rs 00000000011101001111111110000000 0x0074FF80 im ················0000000011001000 ····0xC800 ---------------------------------------------- rd 00000000011101010000000001001000 0x00750048

SUB will subtract from rs the value of rt and store the result in rd.

SUB rd, rs, st [rd = rs - rt] SUB rd, 0x00000000, 0x00000000 rs 00000000000000000000000000000000 0x00000000 rt 00000000000000000000000000000000 0x00000000 ---------------------------------------------- rd 00000000000000000000000000000000 0x00000000

SUBU rd, rs, st [rd = rs - rt] SUBU rd, 0x00000000, 0x00000000 rs 00000000000000000000000000000000 0x00000000 rt 00000000000000000000000000000000 0x00000000 ---------------------------------------------- rd 00000000000000000000000000000000 0x00000000

ASM Hacking & Debugging with pSX

In this example we're going to edit the formula 0x53, which is originally:
Dmg_(Y%) Hit_(MA+X%)
and transform it into
Dmg_(PA*Y) Hit_(MA+X%)

Because of lazyness and the lack of zodiac compatibility already present in the formula, the outcome of this tutorial will be perfect damage.
This means the damage cannot be increased or lowered in any way. This is only an example.

First let's set a dummy ability for testing. The skill of choice, is as always, Cure. Make a new fresh PSX patch.



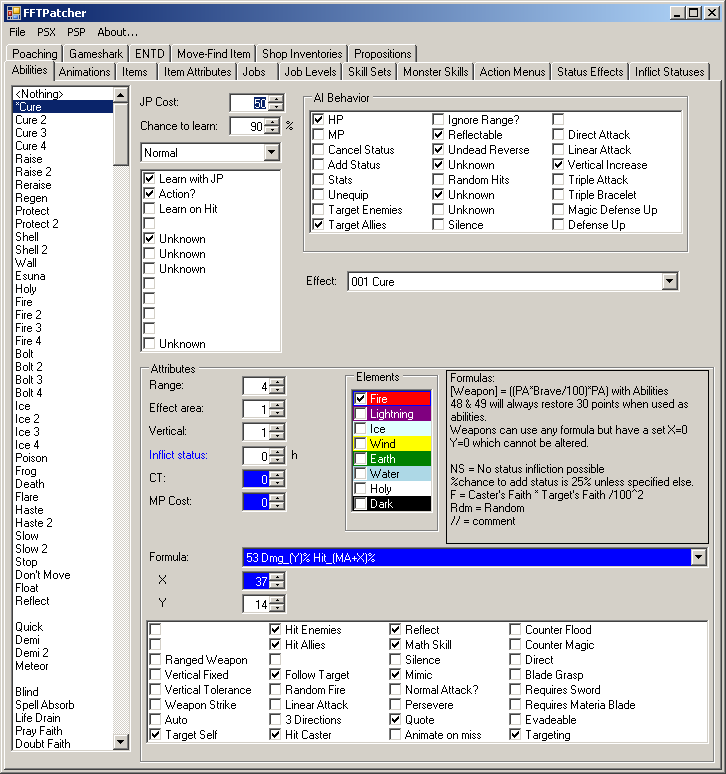
Now that you have made your changes, go to the gameshark tab and note the addresses, which means the first part of the address. The other half is unimportant for now.



Open the debugger and the memory window. Now head to your first address. To do that, press ctrl+g when the memory address is active, and type 0x5FC05.



Now enter the values manually. Remember, a gameshark code starting with "3" affects ONE byte, while a gameshark code starting with "8" affects TWO bytes. DON'T FORGET TO FLIP YOUR BYTES!!



Just checking if you did it right:



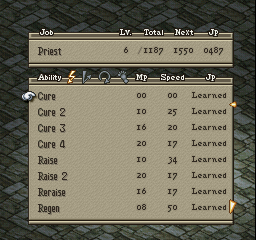
http://www.ffhacktics.com/wiki/Quick_References

Concerning unit stats
OK, a bit ugly, but you'll get the idea.
# Player unit 1 : 0x801924CC : Malak
# Player unit 2 : 0x8019268C : Rafa
# Player unit 3 : 0x8019284C : Meliadoul
# Player unit 4 : 0x80192A0C : Hyudra
# Player unit 5 : 0x80192BCC : Orlandu

It's always better to know your unit IDs before entering the battle, it saves searching time.

Too bad this won't be of any use in this tutorial, but it's very good to know.



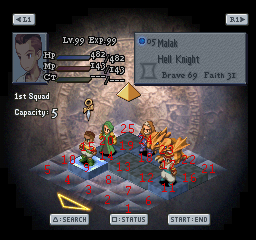
Now take your unholy cure spell and prepare to target someone, make a quicksave here.



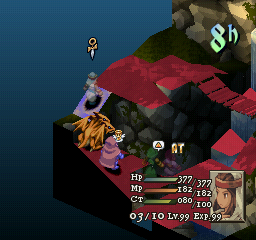
Time to add a breakpoint. To do this, right click inside the breakpoint window.



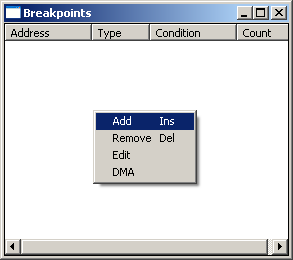
It will be Cure's Y value. It will be read and stored before the formula uses it. You can use FFTPatcher to get the memory address again if you forgot it.



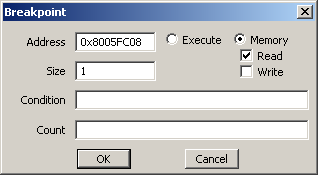
If you look carefully, the byte is loaded and stored again. It was coded this way to always have the X/Y value and other stuff used in a formula at a static location. We simply have to check its next destination, which is 0x801938FA.
This will be our new breakpoint. So edit it.




I made a square to delimitate the formula routine. It's pretty simple, like anything, it starts after another routine ends (after the jr r31) and ends with one.



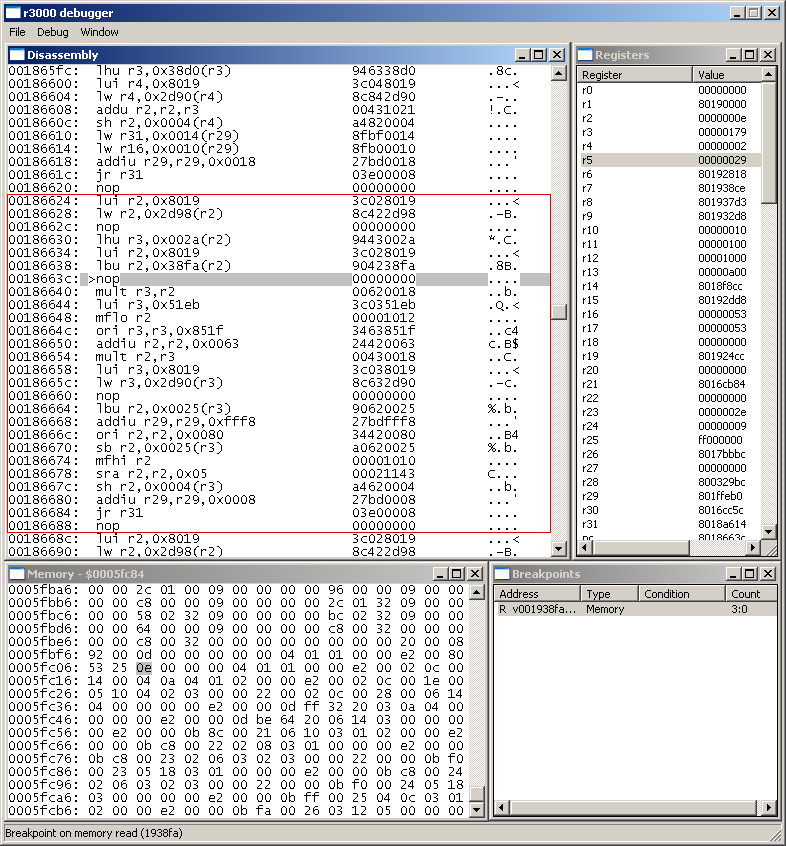
00186624: 3c028019 lui r2,0x8019
00186628: 8c422d98 lw r2,0x2d98(r2)
0018662c: 00000000 nop
>> r2 = Target's stat offset (see http://www.ffhacktics.com/wiki/Formula_Hacking)

00186630: 9443002a lhu r3,0x002a(r2)
>> r3 = Target's Max HP (see http://www.ffhacktics.com/wiki/Formula_Hacking)
00186634: 3c028019 lui r2,0x8019
00186638: 904238fa lbu r2,0x38fa(r2)
0018663c: 00000000 nop
>> r2 = Current ability's "Y"

00186640: 00620018 mult r3,r2
00186644: 3c0351eb lui r3,0x51eb
00186648: 00001012 mflo r2
0018664c: 3463851f ori r3,r3,0x851f
00186650: 24420063 addiu r2,r2,0x0063
00186654: 00430018 mult r2,r3
>> Some complex stuff to calculate % and round up

00186658: 3c038019 lui r3,0x8019
0018665c: 8c632d90 lw r3,0x2d90(r3)
00186660: 00000000 nop
00186664: 90620025 lbu r2,0x0025(r3)
00186668: 27bdfff8 addiu r29,r29,0xfff8
0018666c: 34420080 ori r2,r2,0x0080
00186670: a0620025 sb r2,0x0025(r3)
>> store r2 = Some value for later use?

00186674: 00001010 mfhi r2
>> r2 = calculated % HP damage

00186678: 00021143 sra r2,r2,0x05
0018667c: a4620004 sh r2,0x0004(r3)
>> r2 = r2 divided by 32

00186680: 27bd0008 addiu r29,r29,0x0008
>> no idea

00186684: 03e00008 jr r31
00186688: 00000000 nop
>> Jump return


now let's code some asm to convert Y% damage to PA*Y:

.org 0x80186640
lui r3, 0x8019
lw r3, 0x2D94
lbu r3, 0x0036(r3) (see http://www.ffhacktics.com/wiki/Formula_Hacking)
>> r3 = Caster's PA

mult r2, r3
>> Caster's PA * Y


Now you need to compile this code. Personally I use Renegade64 because I have no idea what other program can compile MIPS r3000.



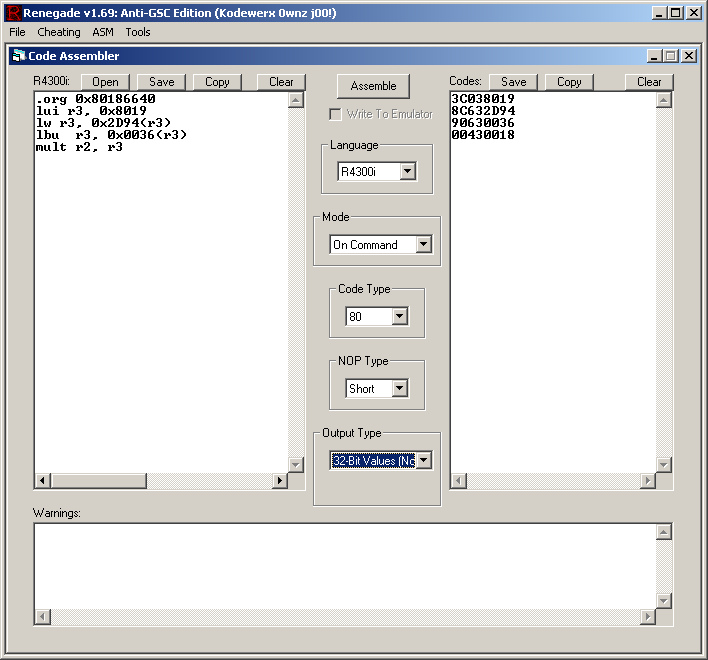
And you need to flip the bytes because Renegade compiled that way... yes, it's a lot of trouble but we don't have much other choice. If you're good with excel you can save some time, unless you really don't have much opcodes like this one.
3C038019
8C632D94
90630036
00430018
becomes
1980033C
942D638C
36006390
18004300

We also need to change "mfhi r2" to "mflo r2"
We should also fill everything else that affects r2 with nop (0x00000000).

Our memory hack should look like this:

0x80186640
1980033C
942D638C
36006390
18004300
00000000
00000000

0x80186674
12100000
00000000

Now to test it, the best way is to use winhex and use your savestate right before taking the action.
However, very often the addresses in quicksaves are 0x02B0 higher than memory addresses.
Meaning you will have to paste your data at:
0x80186640 > 1868F0
and
0x00186678 > 186928

Note that winhex doesn't support "0x" in front of hex. Now load your savestate, make sure you are in hex mode. If you aren't, click the address column.
Press alt+g and enter 1868F0. OK.
Now copy/write the new code. To write, press ctrl+b. It's like paste but it will simply overwrite the present data instead of moving it onwards.



Load your savestate.



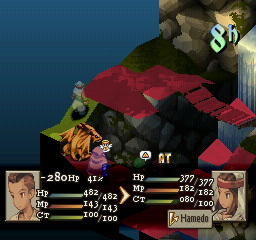
Test.



Victoly!

Now since this is only a formula hack, converting the addresses to BATTLE.BIN is easy. Just subtract 0x67000.

Here's the final Hack:

BATTLE.BIN

0x0011F640
1980033C
942D638C
36006390
18004300
00000000
00000000

0x0011F674
12100000
00000000